MEG data processing

Overview of data processing

The idea with processing the meg data is that within the somewhat random signal that we get as raw data from the MEG, lies multiple levels of fundamental information about the processing that is taking place in the brain. Some light was shed on the most common variables of interest in the last section but let’s go a bit further into the data processing steps we must take to get these clear variables from the continuous raw meg data.

In principal the MEG raw data is composed of a brain signal component and a noise component. Some of the data processing steps, mainly the preprocessing tries to best attenuate the noise component. After the data has been preprocessed, we can move on to the brain signal processing to try and extract pieces of information about the brain processes.

Preprocessing methods

MEG data is notorious for being prone to record noisy raw data. To combat this, there are some hardware and software processes that combat this problem.

Hardware

On the hardware side of the problem, we try to attenuate faraway noise with the Magnetically Shielded Room (MSR), Internal Active Shielding (IAS) and gradiometer sensor arrays.

The MSR (Magnetically shielded room) is comprised of thick layered walls typically made of aluminum and mu-metal. Aluminum has high-conductivity, so higher frequency magnetic fields induce eddy-currents in the walls, thus opposing the entering magnetic field. Mu-metal has high-permeability, so low frequency external magnetic fields are repelled from entering the MSR. At times the MSR walls can be imbedded with additional coil structures to form active compensation systems, but this is not routinely used in MEG.

IAS (Internal Active Shielding) refers to the task of inserting active sensors in the MEG helmet, further away from the head to sample the ambient magnetic field. Because the noise is most likely from a strong faraway source, this recording can then be used to extract the noise time-series from the actual sensor data.

Sensor design is used to attenuate non-neural magnetic fields. Gradiometers, as outlined earlier, work by having a pickup-coil and a compensating coil further from the head. The compensating and pickup-coils are wound in the opposite directions. A faraway magnetic field would in essence cancel itself in the gradiometer coil geometry. This leads to some unwanted attenuation of brain signals.

Software

On the software side we have many ways to attenuate noise. In the MEG-device during online recording we often use Signal-Space Projection (SSP) to clean the data. Offline we start a more robust data processing regimen. There are multiple steps and ways to attenuate noise offline. A few of the most common ones are Signal-Space Separation (SSS), temporal Signal-Space separation (SSS), excluding or extrapolating bad channels, filtering, Independent Component Analysis (ICA). With the right combination of these we can attenuate much of the biological and nearby noise.

SSP works by applying a constant orthogonal vector transformation to the data. The principal vector of any given noise subspace is calculated and then the MEG-data can be projected to a perpendicular signal subspace plane. This gets rid of a lot of noise and some of the relevant brain signals also. The method is fast and can be applied to on-line data.

SSS (Signal-Space Separation) is derived from the Maxwell’s equations of classical electromagnetism. The idea is that the space inside the MEG-helmet and the space outside the helmet can be differentiated by calculating the magnetic fields that inhabit the inside (S_in­) and the outside (S_out­) spaces we can then recalculate the data and exclude the external magnetic fields.

TSSS (temporally-extended Signal-Space Separation) is the temporal extension of the SSS algorithm. The main benefit is that it is more robust and narrows the gap between the S_in­ and S_out­ spaces even further. The TSSS is a much heavier algorithm and thus takes a lot of time in comparison. The TSSS and SSS algorithms are proprietary technology of MEGIN, but recently there have been MATLAB versions of the algorithms to use with other MEG instrumentation. The algorithms are used with the MEGIN software Maxfilter.

Moving the head position offline is possible with Maxifilter when using the (t)SSS algorithms. The program gives the user the option of utilizing the Maxmove algorithms. There are different ways in which the MEG data can be transformed to a different position in the orthogonal 3d space. The data can be transformed to a reference position (0,0,-40 mm) or the first measurement of the file or even the first position of another file. These help with comparing different data sets of a long measurement or even different subjects as a grand average.

Bad channels can be noted during the acquisition phase of the study or they can be visually inspected from the off-line data. There are also automatic algorithms that get rid of bad channels, e.g., Maxfilter Autobad.

Filtering is another great way to handle oscillatory noise or slow-moving periodic drifts. Data can be filtered to include/exclude a specific frequency band. The typical brain responses one might look at with MEG reside in the 7-70 Hz range. Of course, there is brain activity outside this range, namely very high gamma activity. Filtering can be done with a wide variety of methods. The time-series data can be filtered with different types of filters: pass-band, low-pass, high-pass and combs being quite common (Image 15). The name denotes function: low- and high-pass let low or high frequencies pass respectively and a pass-band lets a distinct band of signals pass through. A notch-filter is a particularly narrow pass-band-filter, e.g., 50 Hz. A comb-filter is a combination of high-pass-low-filters.

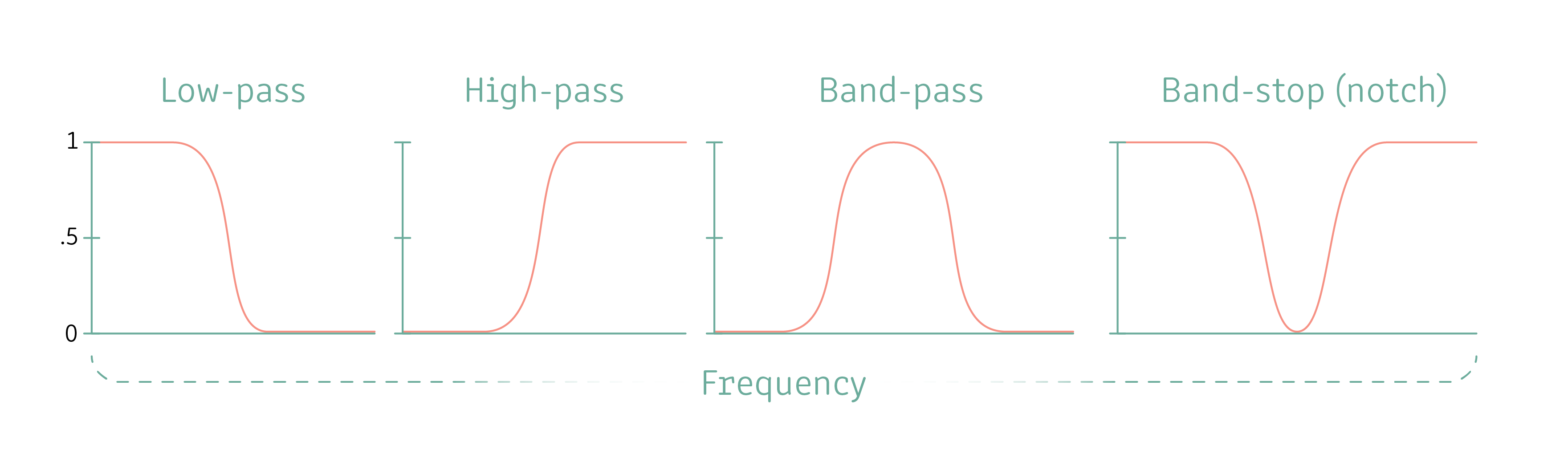
Image 15. A visual representation of some different filter designs. The y-axis representing the proportion of the frequency that is present after filtering.

Filters are an excellent tool to get rid of unwanted noise. The problem being that filtering can also induce artefacts into the data. The main problems with filtering are phase delay or advance, filter induced ringing (attenuates some fqs and accentuates others). Many of the problems can be addressed with modern digital filters, but still some decisions must be made regarding what characteristics (phase, amplitude, etc.) of the data to preserve and which to trade for efficient filtering. A good initial analog acquisition pass-band is 0.01-200 hz with later digital filtering to the wanted pass-band. Further reading about filters.

ICA (Independent Component Analysis) is a modern blind-source approach to MEG artefact rejection. Many artefacts, such as blinks and heartbeat, have a somewhat distinct spatiotemporal signal form. ICA decomposition breaks down the signal into an arbitrary number of signal components that explain a set percentage of the variance of the data, usually around 95 %. The components can then be analyzed, and unwanted components discarded. After discarding, say blinks and cardiac artefacts, the data can then be recomposed with the rest of the components. The ICA can be somewhat described as listening to a recording of multiple instruments and then decomposing the audio data to each instrument respectively.

For the detection and removal of physiological artifacts in the MEG data, such as those related to eye movement and blinks, cardiac cycle, and muscle activity, it is helpful to record electrooculogram (EOG), electrocardiogram (ECG), and electromyogram (EMG) data simultaneously with MEG.

Evoked responses

The simplest form of brain response in the continuous meg-data is the phase-locked brain response to a stimulus. Say you flash an image in the visual field of the subject. The subject’s brain will then almost instantaneously exhibit a characteristic brain signal deflection in response to the stimulus. The response is best seen by the sensors overlying the occipital lobe, aka the visual cortex.

This event related phase-locked response is usually hidden by random brain noise, oscillatory activity, and external noise. Thus, the response is best seen by averaging a good amount of responses in the time-domain. A good amount is 60-70 good, artefact free, stimulations.

This type of analysis / data processing allows us to look at the phase locked deflections in the data. These have been extensively studied and remain an active target for further research.

Power spectra and frequency-domain data

A common mathematical basis for handling time-series data, e.g., meg data with n number of data points with a time and power value, is the use of Fourier transformation. The Fourier series are a way of representing any continuous data using summed sine and cosine waves. The Fourier transformation is an application of the Fourier series. It is a mathematical way of transforming time domain data into its frequency domain representation. There are also discrete-time Fourier transforms, which are used for data in distinct samples, e.g., digital meg signal data (samples per second).

The Fourier transformation in its original form is a computation heavy operation. It is somewhat useful to use with short data segments, but the computational demands increase exponentially with the increasing time segment length. thus, signal processing applications, like meg data analysis, utilize Fast Fourier Transforms (FFT). The FFT algorithms reduce the complexity of the original Fourier Transformation and thus cut the computational cost of the operation.

---- OSCILLATORY DECOMPOSITION IMAGE ----

The images represent first the theoretical background for the summation of oscillatory components to make a continuous signal of any kind. The FFT then transforms the data to the frequency domain where peaks correspond to the power of an oscillatory component in the original data.

Another thing to remember is the Nyquist frequency that is a ½ of the sampling frequency. That is the highest frequency that can be analyzed because of aliasing problems when going higher.

Looking at a continuous segment of meg data, one can readily feel that there might be oscillatory components in the data that can be described with sine and cosine waves. For example, the alpha oscillations of the visual cortical regions are quite noticeable in resting state data. The meg data itself is just a collection of measured time-series values at a set frequency and cannot themselves be easily used for analysis of the oscillatory components.

By using FFTs and a window estimation method (often Welch method) we can first transform the continuous data to the frequency domain. Then, by averaging sequential overlapping windows of the continuous data, we can smooth the power spectrum. The use of these Hanning windows affects the data so that the smaller the window, the greater the smoothing. This of course reduces the frequency resolution of the data.

Induced responses

Another quite simple metric to look at in the continuous brain signals is the amount of oscillatory activity in the brain at a given moment. The idea with power spectra and spectral analysis is to look at long stretches of data and arrive at a conclusion of the overall oscillatory activity in each dataset.

The induced responses look at the oscillatory activity in the brain in a slightly different manner. The idea is to take timepoints locked to a stimulus or trigger and then calculate the instantaneous effects it has on the oscillatory activity.

Some common ways to approach the analysis is in the same way as in the power spectra. The difference is that we first epoch the data around specific triggers. Preferably we have around 60-70 artefact free trigger events in the data. Then we computationally transform the data from time-domain to the frequency-domain. Then, where the power spectra are power-frequency representations, the induced responses are time-frequency representations. After the transformation of the data, we can then average all the responses to a trigger, resulting in robust frequency-time data.

• Lisätietoa

  test asdas daksd aksjk
  
  asdkasjdaskdkasdkasj
  
  afksjaskfjkajs k